Jeder, zumindest jeder der auf diesen Artikel gestoßen ist, hat sicherlich schon mal etwas von dem Grenzsteuersatz gehört. Er findet in vielen Artikeln die sich mit Steuern beschäftigen Verwendung, aber normalerweise wird immer nur gesagt, dass dieser schwer zu berechnen sei und dass das alles viel zu kompliziert ist um näher drauf einzugehen. Aber so kompliziert ist das gar nicht. In diesem Beitrag werde ich die Hintergründe und die Berechnung des Grenzsteuersatzes erklären und herleiten.
Grenzsteuersatz: Was bedeutet das überhaupt?
Der Grenzsteuersatz soll angeben, wie stark ein zusätzlich verdienter Euro versteuert werden muss. Wenn man z.B. einen Grenzsteuersatz von 20% hat, bekommt man von einem zusätzlich verdienten Euro nur 80 Cent. In den unteren Lohngruppen verhält sich das sogar noch ein bisschen komplizierter, aber darauf gehen wir später ein. Jetzt ermitteln wir erst mal mathematisch die Grenzsteuersätze
Das Einkommenssteuergesetz als Grundlage
Alles Nachfolgende, insbesondere die Berechnungen beziehen sich auf das Jahr 2020. Keine Gewähr für die Richtigkeit der Angaben und Erklärungen. Bei Fehlern oder Fragen, gerne unten kommentieren oder mir eine Mail schreiben.
Die Basis zur Ermittlung des Grenzsteuersatzes liefert natürlich das Einkommenssteuergesetz.
Und zwar der Paragraph §32a Einkommenssteuertarif, https://www.gesetze-im-internet.de/estg/__32a.html
Der besagt folgendes:

Aus diesen fünf Gleichungen und dem nachfolgenden Text, berechnet sich der Steuersatz.
Das schauen wir uns nun mal genauer an. Dazu notieren wir uns erst mal die fünf Gleichungen:
- ok, wenn man „wenig genug“ verdient, zahlt man gar keine Steuern und muss sich keine Gedanken machen
- von 9 409 Euro bis 14 532 Euro:
(972,87 · y + 1 400) · y - von 14 533 Euro bis 57 051 Euro
(212,02 · z + 2 397) · z + 972,79 - von 57 052 Euro bis 270 500 Euro:
0,42 · x – 8 963,74 - von 270 501 Euro an:
0,45 · x – 17 078,74
Der Satz darunter beschreibt, was x, y und z bedeutet. Das müssen wir auch erst mal in einer Gleichung formulieren.
Die Beschreibung der Größen im Gesetzestext ist eigentlich in der falschen Reihenfolge notiert, weil sich y und z auf x beziehen. Daher beginnen wir mit x.
Die Größe „x“ ist das auf einen vollen Euro-Betrag abgerundete zu versteuernde Einkommen
\[ x = zuVersteuerndesEinkommen \]Die Größe „y“ ist ein Zehntausendstel des den Grundfreibetrag übersteigenden Teils des auf einen vollen Euro-Betrag abgerundeten zu versteuernden Einkommens.
Die Größe „z“ ist ein Zehntausendstel des 14 532 Euro übersteigenden Teils des auf einen vollen Euro-Betrag abgerundeten zu versteuernden Einkommens.
\[ z=\frac{x-14532}{10000} \]Nun können wir das x, y und z in die obigen Formeln einsetzen und erhalten folgendes.
Bei der Formel unter zweitens lösen wir erst mal die Klammer auf, dann haben wir es später einfacher.
\[ zweitens = (972,87 · y + 1 400) · y \]
\[ zweitens = 972,87 · y^2 + 1 400 · y \]
Nun setzen wir y ein
\[ zweitens = 972,87 · \left(\frac{x-9408}{10000}\right)^2 + 1400 · \frac{x-9408}{10000} \]Das gleiche machen wir dann bei drittens und setzen dann z ein
\[ drittens= (212,02 · z + 2 397) · z + 972,79 \]
\[ drittens= 212,02 · z^2 + 2 397 · z + 972,79 \]
\[ drittens= 212,02 · \left(\frac{x-14532}{10000}\right)^2 + 2 397 · \frac{x-14532}{10000} + 972,79 \]
Bei viertens und fünftes gibt es nichts einzusetzen, da x ja das zu versteuernde Einkommen ist.
So jetzt haben wir die Formeln mathematisch schön notiert.
Ermittlung der Grenzsteuersätze
Wie oben schon erwähnt, soll angegeben werden, wie stark ein zusätzlich verdienter Euro versteuert werden muss. Wir schauen uns zunächst den mathematisch einfacheren Fall an, dass wären die Tarifzonen 4 und 5. Da sich beide vom Prinzip her nicht unterscheiden, beleuchten wir Tarifzone 4.
0,42 · x – 8 963,74
Das ist der triviale Fall, der Grenzsteuersatz ist einfach 42%. Weil wenn sich x, das zu versteuernde Einkommen, um 1 € erhöht, müssen zusätzlich 42 Cent Steuern gezahlt werden.
Mathematisch betrachtet, erhält man diese 0,42 bzw. 42% durch die erste Ableitung dieser Funktion. Da x keinen Exponenten aufweist, fällt x weg, die Konstante fällt sowieso weg, und wir erhalten einfach 0,42.
Nun schauen wir uns mal die Funktion für die zweite Tarifzone an.
\[ zweitens = 972,87 · y^2 + 1 400 · y \]Hierbei handelt es sich um eine quadratische Funktion, zu erkennen an dem Exponenten 2 an dem y.
Für die Tarifzone 2 sieht die Besteuerung daher so aus. Die Gerade dient dazu, besser zu erkennen, dass es sich um eine quadratische Funktion handelt. Die hinterlegte Berechnung erfolgt in 1 Euro Schritten und es wird nicht gerundet
Den Grenzsteuersatz erhält man auch hier durch die erste Ableitung der Funktion. Die erste Ableitung der Funktion gibt immer die Steigung am jeweils betrachteten Punkt der Kurve wieder, in diesem Fall das zu versteuernde Einkommen. Die erste Ableitung der zweiten Funktion sieht so aus. Als Ausgangspunkt nehmen wir die Funktion wo das y schon ersetzt wurde.
\[ zweitens = 972,87 · \left(\frac{x-9408}{10000}\right)^2 + 1400 · \frac{x-9408}{10000} \]Das einmal abgeleitet und vereinfacht ergibt
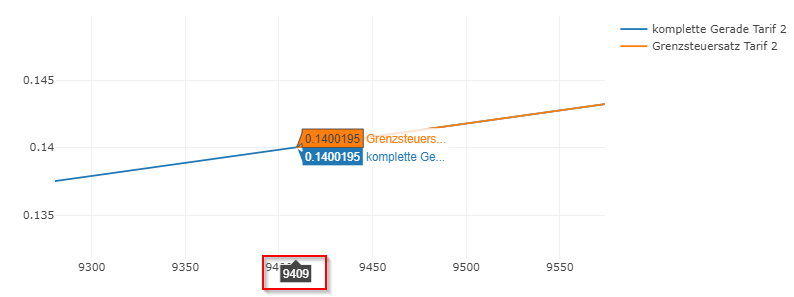
\[ Tarifzone 2, erste Ableitung= 0,0000194574 x - 0,0430552 \]Diese Funktion stellt eine Gerade mit einer Steigung von 0,0000194574 dar und einer Verschiebung auf der y-Achse um 0,0430552. Im nachfolgenden Diagramm ist die komplette Gerade, mit x=0 als Startpunkt, und die Gerade in den Grenzen des Gültigkeitsbereiches für die Tarifzone 2 dargestellt.
Wenn man sich nun den Startpunkt der für den Tarif 2 geltenden Gerade anschaut, sieht man den Eingangssteuersatz von 14% bei 9409 Euro
Das gleiche Spiel kann man dann auch noch für die Funktion für die dritte Tarifzone machen.
\[ Tarifzone 3, erste Ableitung=4,2404 · 10^{-6} · x + 0,178079\]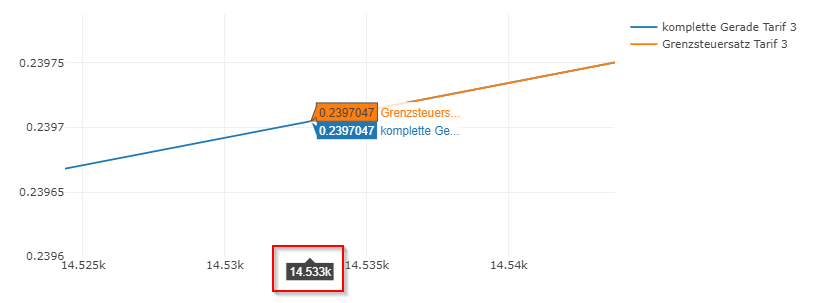
Hier ist jetzt zu erkennen, dass der Eingangssteuersatz für die Tarifzone 3 23,97% beträgt.
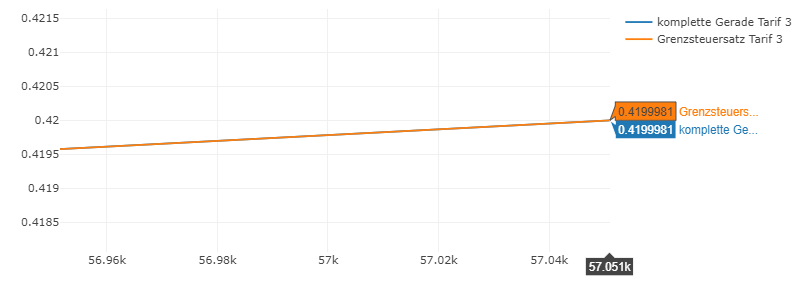
Und der Spitzensteuersatz in dieser Tarifzone ist 41,99 % bei 57051 €. Bei 57052 € beginnt ja der lineare Bereich der Tarifzone 4 mit 42%
Hier sind die Verläufe der Grenzsteuersätze für alle 4 Tarifzonen zusammen dargestellt
Wie kommen die überhaupt auf die Zahlen im Gesetzestext
Jetzt wissen wir wie man über die Formeln aus dem Gesetzestext den Grenzsteuersatz berechnet. Jetzt könnte man sich die Frage stellen, wie der Gesetzgeber überhaupt auf diese komischen Werte in den Formeln kommt. Die Lösung ist, dass die ganze Sache eigentlich von hinten aufgezogen wird.
Es wurden im Vorfeld die Grenzsteuersätze und die Art der Funktionsverläufe festgelegt.
Tarifzone 2
Art der Funktion: quadratisch
Einkommensgrenzen: 9408 - 14532 Euro
Eingangssteuersatz: 14%
Spitzensteuersatz: 23,97 %
Die Grundform einer quadratischen Funktion ist
\[ ax^2 +bx +c \]Da ja die Grenzsteuersätze vorgegeben sind und diese die Steigung der Funktion darstellen, brauchen wir erst mal wieder die erste Ableitung dieser Grundfunktion. Die erste Ableitung der Funktion gibt die Steigung der Ausgangsfunktion in jedem Punkt wieder.
\[ 2ax + b \]Diese Gleichung stellt ja wieder eine Gerade dar, wobei das 2a die Steigung und das b die Verschiebung auf der y-Achse darstellt.
Info:
Die Steigung 2a ist nicht die Steigung der quadratischen Funktion, sondern der Geraden. Die Steigung der quadratischen Funktion ergibt sich aus der gesamten Funktion der Geraden und ist für jeden Wert von x anders.
Die Steigung a ergibt sich nun aus dem Eingangs- und dem Spitzensteuersatz für die Tarifzone.
9409€ -> 14%
14532€ -> 23,97%
Die Steigung ergibt sich aus den beiden Differenzen, da die Besteuerung zwischen 9408 und 14532 Euro von 14% auf 23,97% steigt. Es wird hier mit 9408 und nicht mit 9409 Euro gerechnet, weil die Tarifzone 1 bei 9408 Euro endet.
\[ \frac{0,2397-0,14}{14532 - 9408}=a \]Nun haben wir den Wert von 2a. Um jetzt auf das a zu kommen, müssen wir den Wert natürlich durch 2 teilen
\[ a= 0,00097287\]Wenn man diesen Wert jetzt mit 10000 multipliziert (das wurde im Gesetz nur gemacht, damit man nicht so kleine Zahlen im Text verwenden muss), erhält man die 972,87 aus dem Gesetzestext.
Wenn man das Komma direkt an der richtigen Stelle haben möchte, kann man den Wert auch ermitteln, indem man das zu versteuernde Einkommen und die daraus resultierende Steuer in die einmal abgeleitete Gleichung einsetzt.
\[ 972,87 · y^2 + 1 400 · y \]
y einsetzen
\[ 972,87 · (\frac{x-9408}{10000})^2 + 1 400*(\frac{x-9408}{10000}) \]
für x das maximale Einkommen der Tarifzone 2 einsetzen, 14532 Euro
die darauf zu zahlende Steuer beträgt 23,97% des um 9408 Euro übersteigenden Einkommens
y wird nach x umgestellt, weil wir y ableiten werden
\[ x=y*10000+9408 \]
\[ 972,87 · (\frac{14532-9408}{10000})^2 + 1 400*(\frac{x-9408}{10000}) = 0,2397*(y*10000+9408) \]
einmal nach y ableiten
In dieser Gleichung sind auch alle Eckpunkte enthalten, die man vorher festgelegt hat um die Steuerformeln zu ermitteln
die Einkommensgrenzen 14532 und 9408 Euro, die 14% in Form der 1400 und die 23,97% in Form der 0,2397
\[ 2*a · (\frac{14532-9408}{10000}) + 1400 = 0,2397*10000 \]
nach a auflösen
\[ a= 972,873\]
Tarifzone 3
Art der Funktion: quadratisch
Einkommensgrenzen: 14533 - 57051 Euro
Eingangssteuersatz: 23,97%
Spitzensteuersatz: 42 %
Hier haben wir um Grunde das gleiche Spiel wie bei der Tarifzone 2.
\[ Tarif 3= 212,02 · \left(\frac{x-14532}{10000}\right)^2 + 2 397 · \frac{x-14532}{10000} + 972,79 \]
\[ 2*a * \left(\frac{57051-14532}{10000}\right) + 2397 =0,42*10000 \]
\[ a=212,02\]
Die Steigung zu ermitteln funktioniert hier also genau so wie beim Tarif 2. Allerdings hat der Tarif 3 noch einen Term mehr in seiner Steuerformel, die 972,79, wo kommt das her?
Wenn man in die Formel für Tarif 3 für x 14532 eingibt, werden die Terme die ein x enthalten 0 und die Steuer beträgt 972,79 Euro. Diesen Wert erhält man auch wenn man 14532 in die Formel für den Tarif 2 einträgt.
Die 972,79 Euro bilden den Übergang von der einen Tarifzone in die andere.
Tarifzone 4
Art der Funktion: linear
Einkommensgrenzen: 57052- 270500 Euro
Steuersatz: 42%
In der Tarifzone 4 ist die Besteuerung einfach linear. Daher müssen wir nur schauen wie sich der Term 8963,74 ergibt. Im Grunde genau so wie beim Tarif 3. Dieser Wert bildet den Übergang zwischen Tarifzone 3 und 4.
\[ Tarif 4= 0,42 · x – 8 963,74 \]
\[ Tarif 3= 212,02 · \left(\frac{57051-14532}{10000}\right)^2 + 2 397 · \frac{57051-14532}{10000} + 972,79 =14997,63 \]
\[ Tarif 4= 0,42 · 57051 – 8 963,74 = 14997,68 \]
Tarifzone 5
Art der Funktion: linear
Einkommensgrenzen: ab 270501 Euro
Steuersatz: 45%
\[ Tarif 4= 0,42 · 270500 – 8 963,74 = 104646,26\]
\[ Tarif 5= 0,45 · 270500 – 17 078,74 = 104646,26\]
Ablesen der Besteuerung aus dem Diagramm der Grenzsteuersätze
Es wurde ja schon erwähnt, dass der Grenzsteuersatz angibt, wie stark ein zusätzlich verdienter Euro besteuert wird. In den Tarifzonen 4 und 5 sind es einfach 42% bzw. 45%.
Interessanter verhält es sich in den Zonen 2 und 3, weil wir dort quadratische Funktionen haben und der Grenzsteuersatz sich mit dem Einkommen erhöht.
In der nachfolgenden Tabelle wurde über den Grenzsteuersatz jeweils die anfallende Steuer für den zusätzlich verdienten Euro berechnet. Die Summe daraus plus die Steuer für 14533 Euro ergeben den selben Betrag wie die Steuer die mittels der Steuerformel für 14563 Euro berechnet wurde.
Das Excel-Sheet enthält zwei Tabs, weil die Werte mittels Makros, besser gesagt VBA Funktionen, berechnet werden, aber die Webversion von Excel Makros nicht ausführt (siehe UnterschiedeExcelWebversion). Das Sheet kann jedoch heruntergeladen werden und dann sieht man auch die hinterlegten Berechnungen.
Die Berechnung der Besteuerung jedes einzelnen Euros und die Bildung der Summe daraus entspricht dem Integral der Grenzsteuersatzfunktion. Das Integral der Grenzsteuersatzfunktion ist ja auch wieder die Steuerformel, weil die Grenzsteuersatzfunktion die erste Ableitung (das Differential) der Steuerformel ist.
Das Integral entspricht auch der Fläche unterhalb der Grenzsteuersatzfunktion.
In dem Beispiel unten werden die Flächen zur Besteuerung von 57051 Euro berechnet.
Die Fläche besteht aus dem Trapez zwischen 14533€ und 57051€, dem Dreieck davor zwischen 9409€ und 14533€ und dem Sockel darunter zwischen 9409€ und 57051€
Die Fläche eines Trapezes wird folgendermaßen berechnet. Flächenberechnung für Dreieck und Sockel (Rechteck) sollte bekannt sein.
\[ A=\frac{(a+c)*h}{2} \]\[
a= 0,2397 - 0,14 = 0,0997\\
c = 0,42-0,14 = 0,28\\
h = 57051 - 14532=42519\\
A=\frac{(0,0997+0,28)*42519}{2} = 8072,23215
\]
plus das Dreieck am Anfang
\[
Dreieck = (14533-9408)*0,0997/2=255,48125\]
plus der Sockel
\[Sockel = (57051-9408)*0,14 = 6670,02\\
Summe = 8072,23215+255,48125+6670,02= 14997,7334 Euro\]
Vergleich mit Steuerformel für Tarif 3, gleiches Ergebnis
\[ Tarif3, bei 57051= 212,02 · \left(\frac{57051-14532}{10000}\right)^2 + 2 397 · \frac{57051-14532}{10000} + 972,79 = 14997,63 Euro \]
Anhang
Hier gibt es noch ein paar nette Diagramme im Anhang
Steuer aller 4 Tarifzonen
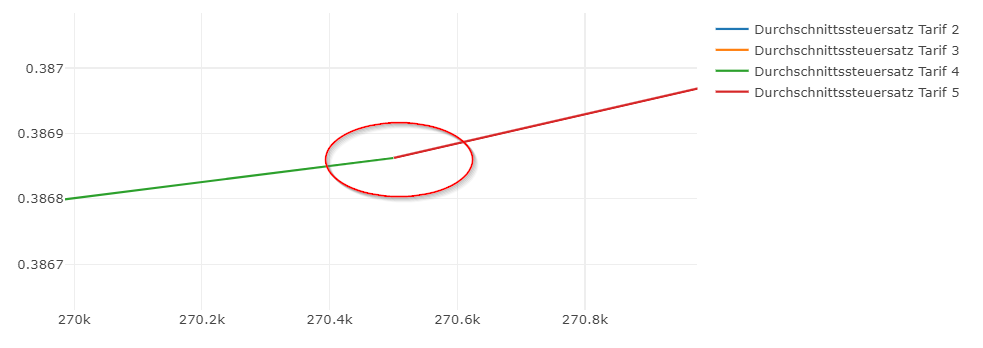
Die Durchschnittssteuersätze
Hier sieht man auch relativ gut den Knick zwischen Tarif 4 und 5, weil plötzlich der Grenzsteuersatz von 42% auf 45% springt.
Die Grenzsteuersätze mit Tooltip über Einkommen, Steuer und Durchschnittssteuersatz